Algorithm

Maximum Subarray Sum

Given a single dimensional array, find the maximum value, a contiguous subarray can have.

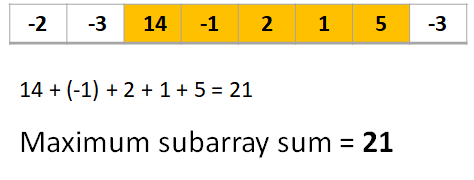
Kadane’s Algorithm for finding the maximum subarray for an one dimensional array in O(n) time.
Note: This algorithm requires at least one positive number, so all negative array is invalid input.

begin
    (maxSum, maxStart, maxEnd) := (-INF, 0, 0)
    currMaxSum := 0
    currStart := 1
    for currEnd := 1 to n do
        currMaxSum := currMaxSum + array[currEnd]
        if currMaxSum > maxSum then
            (maxSum, maxStart, maxEnd) := (currMaxSum, currStart, currEnd)
        endif

        if currMaxSum < 0 then
            currMaxSum := 0
            currStart := currEnd + 1
        endif
    endfor

    return (maxSum, maxStart, maxEnd)
end

Solution: Find max sum

#include <bits/stdc++.h>
using namespace std;

int solve(vector<int>& vec) {
  int current_sum = vec[0];
  int global_sum = vec[0];

  for (int i = 1; i < vec.size(); i++) {
    current_sum = max(vec[i], current_sum + vec[i]);
    global_sum = max(current_sum, global_sum);
  }
  return global_sum;
}

int main() {
  vector<int> vec = {-2, -3, 14, -1, 2, 1, 5, -3};
  cout << solve(vec) << endl;
}
21

Solution: Find max sum along with start and end index

#include <bits/stdc++.h>
using namespace std;

vector<int> solve(vector<int> &vec) {
  int current_sum = 0;
  int global_sum = INT_MIN;
  int max_start = 0;
  int max_end = 0;
  int curr_start = 0;

  for (int i = 0; i < vec.size(); i++) {
    current_sum += vec[i];

    if (global_sum < current_sum) {
      global_sum = current_sum;
      max_start = curr_start;
      max_end = i;
    }

    if (current_sum < 0) {
      current_sum = 0;
      curr_start = i + 1;
    }
  }
  vector<int> result;
  result.push_back(global_sum);
  result.push_back(max_start);
  result.push_back(max_end);
  return result;
}

int main() {
  vector<int> vec = {-2, -3, 14, -1, 2, 1, 5, -3};
  vector<int> res = solve(vec);
  cout << "Max sum: " << res[0] << endl;
  cout << "Start index: " << res[1] << endl;
  cout << "End index: " << res[2] << endl;
}
Max sum: 21 
Start index: 2 
End index: 6

References

Related Posts